 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
template <class T1, class T2> calculated-result-type cyl_bessel_i(T1 v, T2 x); template <class T1, class T2, class Policy> calculated-result-type cyl_bessel_i(T1 v, T2 x, const Policy&); template <class T1, class T2> calculated-result-type cyl_bessel_k(T1 v, T2 x); template <class T1, class T2, class Policy> calculated-result-type cyl_bessel_k(T1 v, T2 x, const Policy&);
The functions cyl_bessel_i and cyl_bessel_k return the result of the modified Bessel functions of the first and second kind respectively:
cyl_bessel_i(v, x) = Iv(x)
cyl_bessel_k(v, x) = Kv(x)
where:
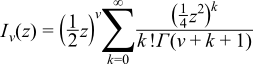
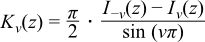
The return type of these functions is computed using the result type calculation rules when T1 and T2 are different types. The functions are also optimised for the relatively common case that T1 is an integer.
The final Policy argument is optional and can be used to control the behaviour of the function: how it handles errors, what level of precision to use etc. Refer to the policy documentation for more details.
The functions return the result of domain_error
whenever the result is undefined or complex. For cyl_bessel_j
this occurs when x <
0 and v is not an integer, or when
x ==
0 and v
!= 0.
For cyl_neumann
this occurs when x <=
0.
The following graph illustrates the exponential behaviour of Iv.

The following graph illustrates the exponential decay of Kv.

There are two sets of test values: spot values calculated using functions.wolfram.com, and a much larger set of tests computed using a simplified version of this implementation (with all the special case handling removed).
The following tables show how the accuracy of these functions varies on various platforms, along with a comparison to the GSL-1.9 library. Note that only results for the widest floating-point type on the system are given, as narrower types have effectively zero error. All values are relative errors in units of epsilon.
Table 41. Errors Rates in cyl_bessel_i
|
Significand Size |
Platform and Compiler |
Iv |
|---|---|---|
|
53 |
Win32 / Visual C++ 8.0 |
Peak=10 Mean=3.4 GSL Peak=6000 |
|
64 |
Red Hat Linux IA64 / G++ 3.4 |
Peak=11 Mean=3 |
|
64 |
SUSE Linux AMD64 / G++ 4.1 |
Peak=11 Mean=4 |
|
113 |
HP-UX / HP aCC 6 |
Peak=15 Mean=4 |
Table 42. Errors Rates in cyl_bessel_k
|
Significand Size |
Platform and Compiler |
Kv |
|---|---|---|
|
53 |
Win32 / Visual C++ 8.0 |
Peak=9 Mean=2 GSL Peak=9 |
|
64 |
Red Hat Linux IA64 / G++ 3.4 |
Peak=10 Mean=2 |
|
64 |
SUSE Linux AMD64 / G++ 4.1 |
Peak=10 Mean=2 |
|
113 |
HP-UX / HP aCC 6 |
Peak=12 Mean=5 |
The following are handled as special cases first:
When computing Iv for x < 0, then ν must be an integer or a domain error occurs. If ν is an integer, then the function is odd if ν is odd and even if ν is even, and we can reflect to x > 0.
For Iv with v equal to 0, 1 or 0.5 are handled as special cases.
The 0 and 1 cases use minimax rational approximations on finite and infinite intervals. The coefficients are from:
While the 0.5 case is a simple trigonometric function:
I0.5(x) = sqrt(2 / πx) * sinh(x)
For Kv with v an integer, the result is calculated using the recurrence relation:
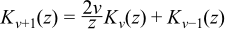
starting from K0 and K1 which are calculated using rational the approximations above. These rational approximations are accurate to around 19 digits, and are therefore only used when T has no more than 64 binary digits of precision.
When x is small compared to v, Ivx is best computed directly from the series:

In the general case, we first normalize ν to [0, [inf])
with the help of the reflection formulae:


Let μ = ν - floor(ν + 1/2), then μ is the fractional part of ν such that |μ| <= 1/2 (we need this for convergence later). The idea is to calculate Kμ(x) and Kμ+1(x), and use them to obtain Iν(x) and Kν(x).
The algorithm is proposed by Temme in N.M. Temme, On the numerical evaluation of the modified bessel function of the third kind, Journal of Computational Physics, vol 19, 324 (1975), which needs two continued fractions as well as the Wronskian:
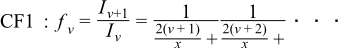


The continued fractions are computed using the modified Lentz's method (W.J. Lentz, Generating Bessel functions in Mie scattering calculations using continued fractions, Applied Optics, vol 15, 668 (1976)). Their convergence rates depend on x, therefore we need different strategies for large x and small x.
x > v, CF1 needs O(x) iterations to converge, CF2 converges rapidly.
x <= v, CF1 converges rapidly, CF2 fails to converge
when x -> 0.
When x is large (x > 2), both continued fractions converge (CF1 may be slow for really large x). Kμ and Kμ+1 can be calculated by

where

S is also a series that is summed along with CF2, see I.J. Thompson and A.R. Barnett, Modified Bessel functions I_v and K_v of real order and complex argument to selected accuracy, Computer Physics Communications, vol 47, 245 (1987).
When x is small (x <= 2), CF2 convergence may fail (but CF1 works very well). The solution here is Temme's series:
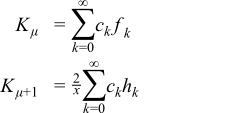
where
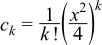
fk and hk are also computed by recursions (involving gamma functions), but the formulas are a little complicated, readers are referred to N.M. Temme, On the numerical evaluation of the modified Bessel function of the third kind, Journal of Computational Physics, vol 19, 324 (1975). Note: Temme's series converge only for |μ| <= 1/2.
Kν(x) is then calculated from the forward recurrence, as is Kν+1(x). With these two values and fν, the Wronskian yields Iν(x) directly.