 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
#include <boost/math/special_functions/expint.hpp>
namespace boost{ namespace math{ template <class T> calculated-result-type expint(T z); template <class T, class Policy> calculated-result-type expint(T z, const Policy&); }} // namespaces
The return type of these functions is computed using the result
type calculation rules: the return type is double if T is an integer type, and T otherwise.
The final Policy argument is optional and can be used to control the behaviour of the function: how it handles errors, what level of precision to use etc. Refer to the policy documentation for more details.
template <class T> calculated-result-type expint(T z); template <class T, class Policy> calculated-result-type expint(T z, const Policy&);
Returns the exponential integral of z:


The following table shows the peak errors (in units of epsilon) found on various platforms with various floating point types, along with comparisons to Cody's SPECFUN implementation and the GSL-1.9 library. Unless otherwise specified any floating point type that is narrower than the one shown will have effectively zero error.
Table 50. Errors In the Function expint(z)
|
Significand Size |
Platform and Compiler |
Error |
|---|---|---|
|
53 |
Win32, Visual C++ 8 |
Peak=2.4 Mean=0.6 GSL Peak=8.9 Mean=0.7 SPECFUN (Cody) Peak=2.5 Mean=0.6 |
|
64 |
RedHat Linux IA_EM64, gcc-4.1 |
Peak=5.1 Mean=0.8 |
|
64 |
Redhat Linux IA64, gcc-4.1 |
Peak=5.0 Mean=0.8 |
|
113 |
HPUX IA64, aCC A.06.06 |
Peak=1.9 Mean=0.63 |
It should be noted that all three libraries tested above offer sub-epsilon precision over most of their range.
GSL has the greatest difficulty near the positive root of En, while Cody's SPECFUN along with this implementation increase their error rates very slightly over the range [4,6].
The tests for these functions come in two parts: basic sanity checks use spot values calculated using Mathworld's online evaluator, while accuracy checks use high-precision test values calculated at 1000-bit precision with NTL::RR and this implementation. Note that the generic and type-specific versions of these functions use differing implementations internally, so this gives us reasonably independent test data. Using our test data to test other "known good" implementations also provides an additional sanity check.
For x < 0 this function just calls zeta(1, -x): which in turn is implemented in terms of rational approximations when the type of x has 113 or fewer bits of precision.
For x > 0 the generic version is implemented using the infinte series:
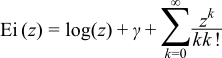
However, when the precision of the argument type is known at compile time and is 113 bits or less, then rational approximations devised by JM are used.
For 0 < z < 6 a root-preserving approximation of the form:

is used, where z0 is the positive root of the function, and R(z/3 - 1) is a minimax rational approximation rescaled so that it is evaluated over [-1,1]. Note that while the rational approximation over [0,6] converges rapidly to the minimax solution it is rather ill-conditioned in practice. Cody and Thacher [5] experienced the same issue and converted the polynomials into Chebeshev form to ensure stable computation. By experiment we found that the polynomials are just as stable in polynomial as Chebyshev form, provided they are computed over the interval [-1,1].
Over the a series of intervals [a,b] and [b,INF] the rational approximation takes the form:

where c is a constant, and R(t) is a minimax solution
optimised for low absolute error compared to c. Variable
t is 1/z when
the range in infinite and 2z/(b-a)
- (2a/(b-a) + 1) otherwise: this has the effect of scaling
z to the interval [-1,1]. As before rational approximations over arbitrary
intervals were found to be ill-conditioned: Cody and Thacher solved this
issue by converting the polynomials to their J-Fraction equivalent. However,
as long as the interval of evaluation was [-1,1] and the number of terms
carefully chosen, it was found that the polynomials could
be evaluated to suitable precision: error rates are typically 2 to 3 epsilon
which is comparible to the error rate that Cody and Thacher achieved using
J-Fractions, but marginally more efficient given that fewer divisions are
involved.
[5] W. J. Cody and H. C. Thacher, Jr., Rational Chebyshev approximations for the exponential integral E1(x), Math. Comp. 22 (1968), 641-649, and W. J. Cody and H. C. Thacher, Jr., Chebyshev approximations for the exponential integral Ei(x), Math. Comp. 23 (1969), 289-303.